Supplement to “Sidereal Time and Universal Time are rotational”
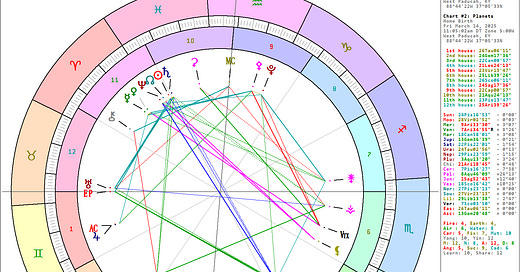
To facilitate deciphering the time conversion formulas, we present two example charts from image #1 here where the Astrolog macro (Thanks! to Walter Pullen) is implemented to combine into one wheel the proper house structure and planets that all other astrological programs (mostly Swiss Ephemeris (SE)-based) are unable presently to generate. Both charts are for the same longitude but for adjacent time zones – EST and CST, with daylight time in effect. Chart #1 is for West Paducah, KY, which is west of the Eastern time zone meridian, and Chart #2 is for Metropolis, IL, which is east of the Central time zone meridian.
Given the equation in the Explanatory Supplement to the Astronomical Almanac, p. 74 (local mean time = universal time - longitude) and considering that clocks are not set using LMT anymore but rather for standard time (i.e., local civil time), with these formulas and with the clocks set as indicated as the starting points, what would (giving the same respect to the longitude of the observer as in this equation) the universal time (UT1) be on which is based the Moon position?
Example Chart #1:
March 14, 2025, 12:00 pm EDT
West Paducah, KY - Long. 88°44'22.53"W, Lat. 37°05'33.35"N
1 - standard time = universal time - time-zone offset + LMT variation
2 - universal time = standard time + time-zone offset - LMT variation
3 - local mean time = universal time - longitude (distance in time from Greenwich)
Answer: 15:05:02.5 UT1
1 - 12:00:00 = 15:05:02.5 - 4:00:00 + 00:54:57.5 (Moon = 28° Vir 02'52.25")
2 - 15:05:02.5 = 12:00:00 + 4:00:00 - 00:54:57.5 (Moon = 28° Vir 02'52.25")
3 - 10:05:02.5 = 16:00:00 - 5:54:57.5 (no daylight time) (Moon = 28° Vir 30'25")
JPL Horizons calculation of the Moon’s longitude:
Example Chart #2:
March 14, 2025, 11:00 am CDT
Metropolis, IL - Long. 88°44'22.53"W, Lat. 37°09'57.57"N
1 - standard time = universal time - time-zone offset - LMT variation
2 - universal time = standard time + time-zone offset + LMT variation
3 - local mean time = universal time - longitude (distance in time from Greenwich)
Answer: 16:05:02.5 UT1
1 - 11:00:00 = 16:05:02.5 - 5:00:00 - 00:05:02.5 (Moon = 28° Vir 32'56.87")
2 - 16:05:02.5 = 11:00:00 + 5:00:00 + 00:05:02.5 (Moon = 28° Vir 32'56.87")
3 - 10:05:02.5 = 16:00:00 - 5:54:57.5 (no daylight time) (Moon = 28° Vir 30'25")
JPL Horizons calculation of the Moon’s longitude: